Formål

Forsøget viser, hvordan man kan måle lydens udbredelseshastighed i atmosfærisk luft. Forsøget laves ved hjælp af en ultralydsender og en mikrofon.

Udstyr
Til forsøget anvendes et oscilloskop med to indgangskanaler. Den ene indgang skal vise ultralydsenderens signal, og den anden viser signalet, som mikrofonen modtager. Begge på en tidsakse (f.eks. 25 mikrosekunder per division). Ultralydsenderens frekvens F er tæt på 40.000 Hz = 40 kHz. Da lydens hastighed C er ca. 340 m/s, kan man fra grundformlen finde bølgelængden L:

C = F L L = C/F = 340/40000 = 0,00850 m = 8,50 mm.

På grund af den korte bølgelængde er en skydelære velegnet instrument til afstandsmålingerne. Sender og modtager kan fastgøres til skydelæren som vist i Figur 1.

Med skydelæren kan man måle afstande med en præcision på 0,1 mm.

Målemetode

Når man flytter på skydelæren, kan man aflæse afstande samtidig med, at man iagttager faseskifte mellem lydsignalet målt fra kilden og lydsignalet målt med mikrofonen. Disse signaler er vist i Figur 2:

Ét faseskifte kan ses ved, at bølgetoppene fra mikrofonsignalet forskydes én bølgelængde, så bølgetoppene mødes igen. Man skal notere afstandene svarende til hvert faseskifte.

Dataanalyse

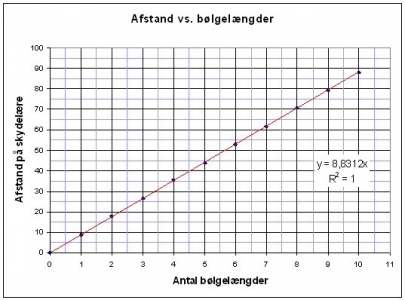
Figur 3 viser typiske resultater for en lydfrekvens F = 39260 Hz. På andenaksen vises afstande svarende til antallet af faseskifte på førsteaksen.

Hældningskoefficienten af grafen svarer til lydens bølgelængde L. I dette eksempel blev L fundet til 8,8312 mm svarende til en lydhastighed på C = F L = 346,7 m/s.

Alternativ målemetode

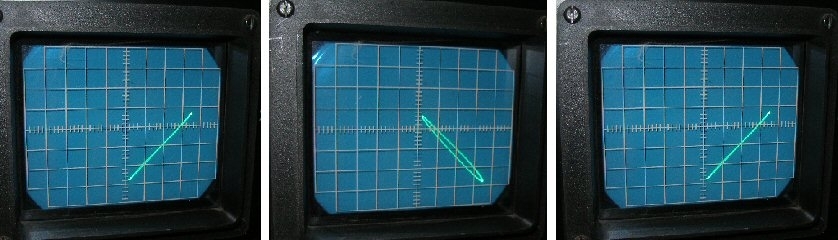
Figur 4 viser en anden mulig målemetode. Indstil oscilloskopet, så lydkildesignalet sluttes til x-aksen, og mikrofonsignalet sluttes til y-aksen. Hermed opstår “Lissajous figurer”. Er begge signaler i fase, opstår en lige linie y = x.

Er signalerne 90 grader ud af fase, dannes en cirkel. Ved faseforskellen 180 grader kommer der en lige linie med hældning minus én: y = -x. Ved 270 grader dannes en cirkel igen, og til sidst kommer den lige linie y = x igen.

Dataanalysen i dette tilfælde er den samme, idet man skal notere sig afstanden mellem faseskifte på 360 grader. Man kan igen lave en graf over afstande og antal faseskifte eller eventuelt finde middelværdien af et antal faseskifteafstande. Når L er fundet, finder man igen lydens hastighed med C = F L.